l’effacement d’erreurs
Bien que la correction de fortes salves d’erreurs soit possible, certains cas de figure dépassent les capacités du CIRC. Ainsi, la présence de trop nombreuses erreurs ou des salves trop importantes est signalée à un circuit d’effacement d’erreurs par le décodeur C2, afin qu’il recalcule les échantillons erronés par interpolation linéaire ou en envoyant un « Mute » si la correction est impossible. Ce circuit d’effacement est externe au CIRC, bien qu’il contribue à la correction globale d’erreurs, sans reconstruction à l’identique.
L’effacement d’erreurs par interpolation permet de traiter jusqu’à 13 000 bits consécutifs, soit 8,5 mm de piste sale ou rayée !
Note : le circuit intégré SAA7000 gère l’interpolation et le muting pour de nombreux lecteurs de première génération. La commande UNEC (Unreliable data) envoyée par l’ERCO (SAA7020) informe le circuit CIM (SAA7000) de l’arrivée d’une trame comprenant des données non corrigées.
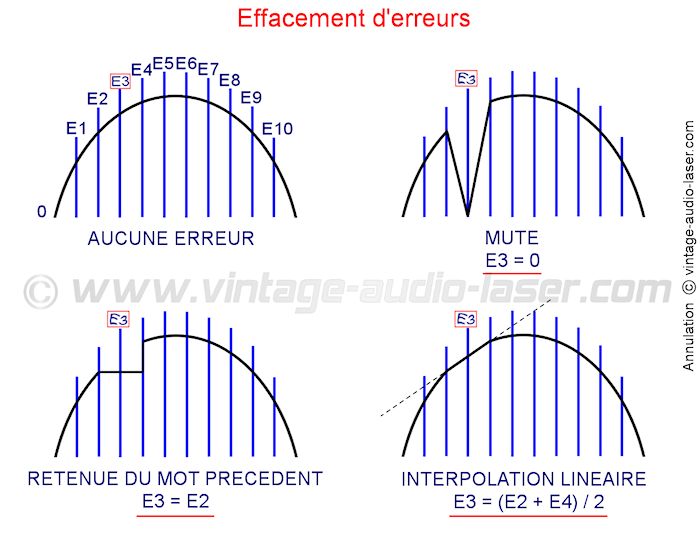
On compte trois procédés d’effacement :
○ Le muting (mise en sourdine)
○ La retenue du mot précédent
○ L’interpolation
Le muting (mise en sourdine)
La mise en sourdine des sorties audio est l’ultime action après que les autres types de correction d’erreurs se sont montrés inefficaces, dans le cas d’une rayure trop longue ou trop large, par exemple. S’il semble logique de couper (« muter ») les sorties audio dans pareil cas, afin d’éviter à l’utilisateur d’entendre le résultat de l’interprétation erronée d’une série d’échantillons, la réalité est moins évidente : la partie endommagée du signal audio ainsi « mutée » peut provoquer un « clic » autrement appelé « glitch » plus dérangeant que le signal altéré lui-même. Au cours de l’élaboration du format « Compact Disc », il fut remarqué que lorsque ce type de « correction » d’erreur était appliqué, associé à un niveau de sortie audio élevé, le résultat pouvait être dommageable pour les haut-parleurs. Quoi qu’il en soit, le Mute est le pire des scénarios, mais un silence est préférable à une interférence numérique audible (clic). Pour éviter le risque de « clic », une atténuation du signal est nécessaire avant et après (fade in) l’action de mise en sourdine afin de rendre la plus brutale des interruptions imperceptible par l’auditeur. En revanche, le Mute de l’échantillon ainsi effacé ne peut être « fabriqué » en mettant tous ses bits à « 0 », car il en résulterait là aussi un « clic » audible. Parmi les méthodes possibles, le signal peut être atténué en multipliant la valeur de l’échantillon précédent par des coefficients graduellement décroissants. De plus, l’atténuation devant précéder l’arrivée du mot défectueux, une ligne à retard est requise avant le circuit de Mute ; l’opération inverse après l’arrivée du mot défectueux permet un effacement absolument indétectable à l’oreille.© vintage-audio-laser.com
Note : le « Mute » réalisé par le circuit de calcul est différent du Mute généré par le microprocesseur (Mute soft), actif pendant les modes « stop », « pause » et « recherche d’index ».
La retenue du mot précédent
En raison des nombreuses opérations effectuées sur le signal RF tout au long de son traitement dans les différents étages, plusieurs mémoires interviennent et le signal se trouve retardé pendant un certain laps de temps. Lors du processus d’enregistrement et de gravure, alors que le signal analogique est échantillonné et que chaque échantillon est converti en mot de 16 bits, nous avons vu que le mot obtenu pouvait prendre une valeur parmi 65 536. Ainsi, il est facile d’imaginer que le mot précédent ou suivant un mot de 16 bits endommagé peut avoir une valeur ne présentant que 1 / 65 536ème de différence avec ce mot. Il est également facile d’imaginer que personne n’est en mesure de constater une différence de timbre ou de hauteur sur une durée de 1 / 44 100ème de seconde (durée d’un échantillon), surtout avec si peu d’écart de valeur entre ces deux mots. Cette solution consistant à recopier le mot précédent pour remplacer un mot endommagé est donc une solution évidente utilisée parmi les différents procédés d’effacement d’erreurs. La retenue du mot précédent intervient si deux mots consécutifs (du même canal, gauche ou droit) sont incorrects.
L’interpolation
La méthode précédente est améliorée par l’interpolation linéaire, qui consiste à calculer la moyenne du mot précédent et du mot suivant le mot erroné, en les additionnant puis en divisant la somme obtenue par deux. Le mot résultant est utilisé pour remplacer le mot défectueux, ce qui constitue une prédiction encore plus performante. L’interpolation intervient si le mot incorrect est encadré par deux mots corrects (du même canal, gauche ou droit).
Résumé des opérations effectuées par le circuit de traitement des données numériques dans le cadre de la correction d’erreurs (un circuit intégré principal pour les lecteurs CD plus récents, trois pour les premiers lecteurs) :
○ Extraction des bits de parité
○ Désentrelacement des symboles audionumériques
○ Détection et corrections des erreurs
○ Calcul par interpolation d’échantillons manquants ou erronés
○ Mute si trop d’échantillons manquants
En sortie du décodeur EFM, les données numériques reconstituées sont envoyées (en liaison série généralement) vers le filtre numérique puis l’étage de conversion numérique / analogique. L’opération complète de décodage est strictement contrôlée par une horloge propre qui est la référence absolue pour la majorité des fonctions du décodeur.
Avant d’aborder le principe de fonctionnement du convertisseur numérique / analogique, il est nécessaire de comprendre le principe de base du codage d’une suite de valeurs analogiques en valeurs numériques. Prenons un exemple parlant de numérisation.
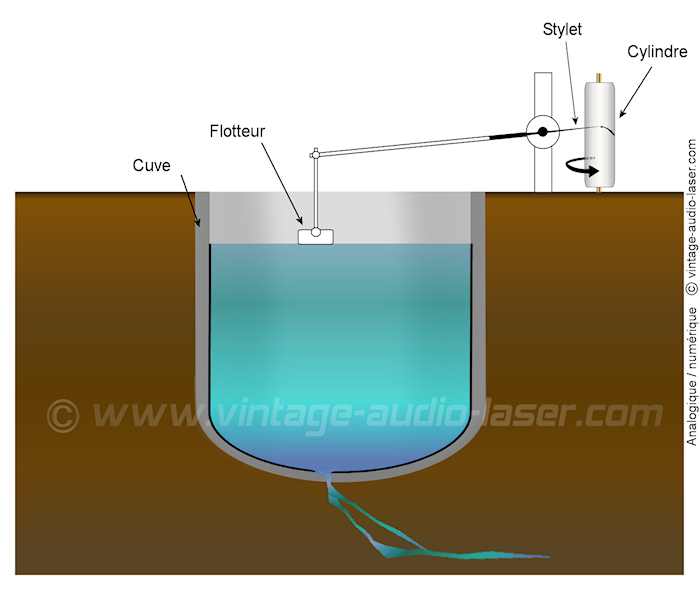
Imaginez que vous deviez tester l’étanchéité d’une petite cuve en béton coulée à même le sol et présentant une légère fissure sur son fond. Pour cela, vous remplissez la cuve d’eau et posez un flotteur à la surface. L’extrémité du flotteur est reliée à un stylet à encre chargé de représenter la courbe correspondant à la lente diminution du niveau d’eau de la cuve. Cette courbe est tracée sur un papier enroulé autour d’un cylindre tournant très lentement, à raison d’une rotation complète au bout de 6 heures. Vous venez d’effectuer une mesure analogique de l’évolution du niveau de liquide dans la cuve.
Cette méthode de mesure analogique permet d’obtenir une représentation plus ou moins fidèle de la quantité d’eau réelle infiltrée dans le sol via la fissure de la cuve. Cette précision dépend de la stabilité mécanique du montage du stylet, du bon écoulement de l’encre, et de la précision de la vitesse de rotation du cylindre. Une accélération progressive de la fuite d’eau due à une dégradation du défaut d’étanchéité doit pouvoir être mesurée sur cet intervalle de 6 heures (rotation complète du cylindre). Malheureusement, toute variation de vitesse de rotation du cylindre se traduira par une variation de la pente de la courbe obtenue et par conséquent à une erreur d’interprétation des mesures. Enfin, si vous devez transmettre ces mesures à une tierce personne éloignée du site de test, vous ne pourrez que lui faire parvenir une copie de la courbe analogique obtenue (fax par exemple) ou bien transmettre verbalement vos impressions ou votre lecture de la courbe (fuite importante en fin de test, progression lente les 30 premières minutes, bref rien de très précis). Si pendant le test vous faites tomber un corps quelconque dans la cuve, un pic suivi d’un amortissement apparaîtra comme un événement anormal difficile à interpréter.
Ce relevé de mesures entièrement analogique contient une infinité de points de mesure sur une durée de 6 heures. Ces mesures incluent toutes les possibilités d’erreur inhérentes au mode opératoire.
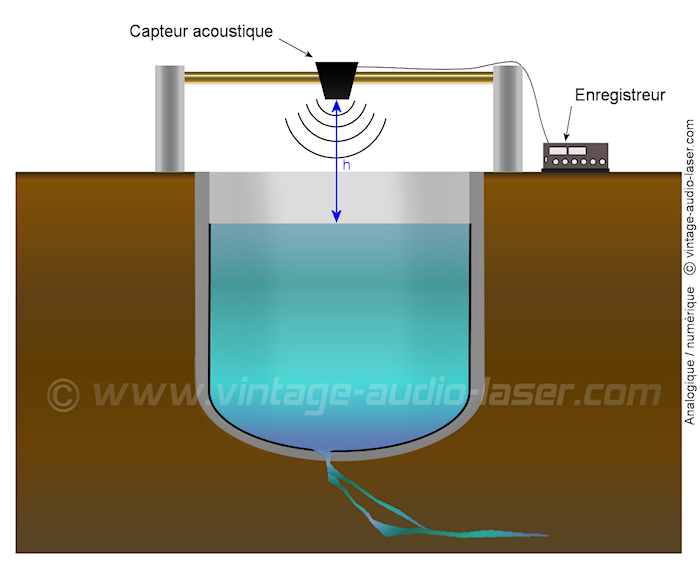
Grand perfectionniste que vous êtes, vous décidez de mettre en œuvre un autre système de mesure, à partir d’un capteur acoustique fonctionnant successivement en émetteur et en récepteur. Le but de l’opération est d’effectuer une suite de mesures à intervalles réguliers (toutes les 5 minutes par exemple). Le capteur est placé au-dessus de la cuve et émet des trains d’ondes acoustiques qui après réflexion sur la surface de l’eau retournent vers le capteur qui les convertit en signal électrique. Chaque mesure correspond au temps mis par l’onde émise pour atteindre le récepteur et dépend de la distance entre le capteur et la surface de l’eau. Un système de mesure automatique valide une mesure toutes les 5 minutes si 10 mesures consécutives dans un laps de temps défini (10 secondes par exemple) ne varient pas de plus de 5 %. Cette sécurité permet de rendre invisible du point de vue de la mesure, l’effet provoqué par la chute du corps étranger évoquée dans la méthode précédente.
Au bout d’un temps défini (5 heures par exemple), vous récupérez un fichier indiquant 72 points de mesure correspondant à l’évolution réelle du niveau d’eau dans la cuve.
Vous venez d’effectuer une mesure numérique de l’évolution du niveau de liquide : ces 72 points de mesure ont été convertis en « 1 » et en « 0 », à partir des mesures analogiques en provenance du récepteur, par l’électronique associée au capteur, et un système d’impression vous permet de récupérer un ticket papier indiquant les mesures en valeurs décimales.

Relevé de mesures
Il vous est possible de transmettre ces mesures par téléphone à un intervenant extérieur qui pourra sans aucun risque d’erreur procéder à une analyse précise de l’importance de la fuite, et envisager ou non une réparation. ©vintage-audio-laser.com
Vous venez de réaliser une numérisation par échantillonnage temporel de données analogiques en prélevant une valeur de hauteur d’eau toutes les 5 minutes. La fréquence d’échantillonnage est de 0,00333 Hz (1 mesure toutes les 300 secondes correspond à 0,00333 mesure par seconde, soit 0,00333 Hz). De la même manière, la fréquence d’échantillonnage utilisée pour le CD correspond à 44 100 Hz, soit 44 100 mesures du signal analogique par seconde, soit 1 mesure tous les 1 / 44 100ème de seconde. Dans tous les cas, la fréquence d’échantillonnage est adaptée au nombre de mesures nécessaires pour une interprétation fidèle du signal analysé. Dans le cas de l’audio, un nombre élevé d’échantillons est indispensable pour envisager une reproduction fidèle du message original.

Pour obtenir une réponse en fréquence plate à 20 kHz, la fréquence d’échantillonnage doit se situer au moins à deux fois cette fréquence haute de la bande passante souhaitée afin d’éviter l’aliasing, que nous verrons plus loin. Avec une fréquence de 44,1 kHz choisie pour de l’échantillonnage, le filtrage à pente raide en aval du convertisseur numérique / analogique dispose de 2 kHz (de 20 à 22 kHz) pour effectuer une atténuation correcte et éliminer le premier sous-harmonique (22,05 kHz) de la fréquence d’échantillonnage.
Toujours en raison de cette fréquence de 44,1 kHz, on sait que l’échantillonnage d’une fréquence pure de 20 kHz ne permet d’obtenir que deux échantillons par période. Ces deux échantillons ne vont permettre de reproduire (lors de la conversion analogique / numérique) qu’un signal carré de fréquence 20 kHz à la place d’un signal sinusoïdal de fréquence 20 kHz. Or, ce signal carré est très différent du signal sinusoïdal. Il est composé d’un ensemble de fréquences, dont la fréquence pure sinusoïdale de 20 kHz et des harmoniques d’ordre supérieur.
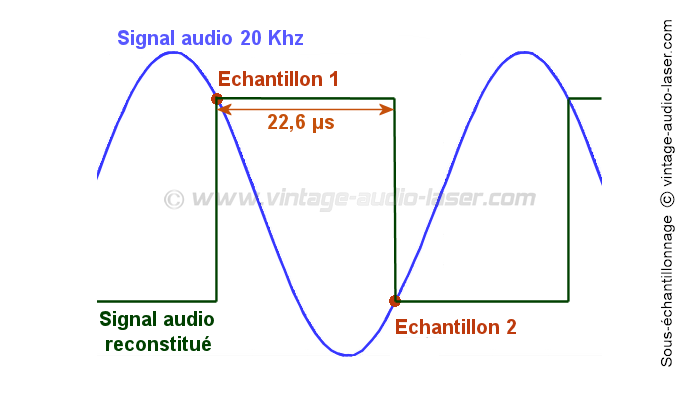
Sous-échantillonnage
Note tous les signaux complexes, autres que sinusoïdaux, sont composés d’une fréquence fondamentale sinusoïdale, et d’une série d’harmoniques (sinusoïdales) multiples de cette fondamentale. Par exemple, un signal de 1 kHz de forme quelconque serait composé d’une fondamentale sinusoïdale d’1 kHz, et d’harmoniques de fréquences 2 kHz, 3 kHz, 4 kHz, etc., indispensables à l’identification de ce signal.
Dans le cas de notre signal carré, il est indispensable de retirer ces harmoniques non souhaités par l’utilisation d’un filtrage à pente raide, ce qui est accompli par un filtre passe-bas utilisé en sortie du convertisseur numérique / analogique, filtre dont voici une utilité autre que l’élimination de l’effet d’aliasing. Au final, malgré l’obtention de deux échantillons par période lors de l’échantillonnage, c’est bien une fréquence pure de 20 kHz qui est restituée, et non un signal carré, conformément au signal analogique d’origine avant numérisation. La difficulté est accentuée lorsque moins de deux échantillons résultent de l’échantillonnage, ce qui a pour effet de créer le fameux « aliasing ».
L’aliasing est une mauvaise réponse d’un système numérique à une fréquence supérieure à la moitié de la fréquence d’échantillonnage, d’après le théorème de Nyquist / Shannon, qui énonce que la fréquence la plus élevée d’un signal à échantillonner ne peut être supérieure à la moitié de la fréquence d’échantillonnage .
Aussi, le premier filtrage est situé à l’entrée du système de numérisation, avant l’échantillonnage. Ce filtre passe-bas à pente très raide, similaire à celui utilisé en sortie du convertisseur N/A du lecteur CD, est chargé d’atténuer au maximum toutes les fréquences supérieures à la moitié de la fréquence d’échantillonnage utilisée pour la numérisation.
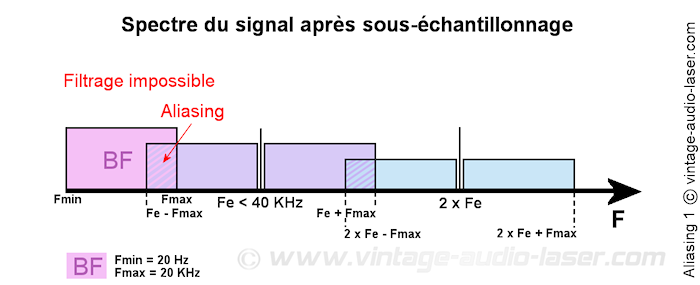
Dans le cas du sous-échantillonnage (moins de deux échantillons pour la fréquence la plus élevée à reproduire), de nouvelles fréquences non désirées sont créées. L’image suivante illustre ce phénomène de fréquence « parasite » :
L’ensemble de ces fréquences non désirées forme « l’aliasing », ou recouvrement. Une représentation spectrale permet de visualiser cet effet.
Afin de minimiser ces interférences, le théorème de Nyquist doit être respecté. Le choix de la fréquence d’échantillonnage 44,1 kHz offre un bon compromis et permet d’éliminer son premier sous-harmonique (22,05 kHz) par l’emploi d’un filtre analogique à pente adaptée. Cependant, la fréquence de coupure du filtre devant se situer entre 20 kHz à 22,05 kHz, un filtre conventionnel LCR ne peut être utilisé sans dégradation de l’extrémité haute de la bande passante (ce qui posait problème avec les premiers lecteurs CD). Nous verrons plus loin que le filtrage numérique est une alternative à ce filtrage périlleux.
Filtrage analogique à pente raide. Dans cet exemple, le théorème de Nyquist est respecté, et un filtrage adapté (brick-wall) permettra de supprimer le spectre « image », après la conversion numérique/analogique : le signal analogique obtenu est passé dans un filtre pour en retirer tout artifice résultant de la fréquence d’échantillonnage (44,1 kHz) qui prendrait la forme d’interférence ou bruit du recouvrement (aliasing)

Chaque échantillon prélevé à partir du signal analogique doit pouvoir être exprimé le plus précisément possible afin de le différencier des échantillons suivants et précédents. Cette précision est directement liée à la quantification, définissant le nombre de bits (« 1 » ou « 0 ») qui va être utilisé pour décrire la valeur prélevée. De la même manière, une valeur décimale à 6 chiffres est plus précise qu’une valeur décimale à 3 chiffres : le nombre Pi peut être écrit 3,14, ou plus précisément 3,14159. Dans le cas du codage PCM utilisé pour le Compact Disc, les valeurs relevées correspondent à l’amplitude du signal audio en Volt à un instant précis. Cette valeur correspond à une durée de 22,6 µs (durée de l’échantillon), ce qui signifie que le codage PCM considère que la valeur mesurée reste la même pendant cet intervalle de temps.
Une quantification sur 16 bits offre 65 536 valeurs de tensions possibles pour un échantillon donné (16 bits => 216 valeurs). Si 0 V correspond à la valeur de tension la plus basse et Vmax à la valeur de tension la plus élevée, on peut déduire que l’écart minimum entre deux valeurs est Vmax ÷ (216 - 1). Cette valeur correspond à la variation provoquée par le changement seul de la valeur du LSB (« 0 » à la place de « 1 », ou inversement).
Ce nombre fini de valeurs numériques produit inévitablement des erreurs dites de quantification. En effet, la reconstitution du signal analogique après échantillonnage et numérisation est effectuée à partir de valeurs approximatives, uniquement représentatives des valeurs analogiques prélevées, car limitées par le nombre de bits affectés à la quantification. Plus ce nombre de bits est élevé, meilleure est la précision. Cependant, la valeur discrète ainsi quantifiée restera toujours une approximation de la valeur mesurée. Par définition, la quantification est la technique d’approximation d’une amplitude analogique par un nombre discret, la plus mauvaise approximation incluant une erreur de la moitié de la résolution du convertisseur, c’est-à-dire un demi-pas de quantification. En d’autres termes, si le passage du bit « 0 » au bit « 1 » du LSB correspond à une variation de 0,5 V alors la valeur quantifiée pourra contenir une erreur maximum de 0,25 V. En théorie, plus il y a de bits, moins l’erreur de quantification est grande, et chaque bit supplémentaire divise le pas d’erreur par 2 ! Cette division par 2 de l’erreur de quantification augmente le rapport signal / erreur (S/E) de 6 dB pour chaque bit supplémentaire (par exemple lorsque la quantification passe de 14 à 15 bits). Du point de vue de l’auditeur, l’erreur de quantification se traduit par une distorsion réelle, bien que difficilement perceptible car située sous le seuil de bruit, dans le cas de la conversion sur 16 bits. Le bruit de quantification dépend non seulement du nombre de bits utilisés, mais aussi de la fréquence de prélèvement d’échantillons associée à ce nombre de bits. Une quantification sur un nombre de bits élevé est inutile si la fréquence d’échantillonnage est trop basse : ceci reflète la problématique rencontrée avec les fréquences les plus élevées du signal analogique à numériser. En effet comme nous l’avons noté précédemment, plus la fréquence du signal analogique à numériser est élevée, moins le signal restitué après conversion N/A en est représentatif : le peu de valeurs obtenues lors de l’échantillonnage d’une fréquence approchant la moitié de la fréquence d’échantillonnage ne permettent qu’une mauvaise approximation du signal original. Ce manque de valeurs discrètes pour reconstituer le signal analogique se traduit par un bruit de quantification plus élevé.
Le bruit de quantification génère des interférences sous forme de pics de bruit aux points d’échantillonnage qui bien que se situant à 44,1 kHz, tendent à dégrader le rapport signal / bruit du lecteur. Plus la fréquence du signal à échantillonner est élevée, plus le signal reconstitué est bruité : les marches formées par la juxtaposition des échantillons obtenus après conversion numérique / analogique sont plus hautes pour un signal de fréquence élevée ; l’amplitude du bruit de quantification est plus grande
exemple de quantification
Admettons que nous devions coder en valeur numérique, sur 16 bits, toutes les valeurs analogiques comprises entre 0 Volts et 10 Volts. Évidemment, cela est impossible, puisque par définition, il existe une infinité de valeurs entre 0 Volts et 10 Volts (3,563459897875… Volts est une valeur au hasard). Aussi devons-nous obligatoirement choisir un nombre maximum de valeurs à convertir en numérique parmi cette infinité de possibilités. Nous pouvons par exemple choisir 11 valeurs : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, et 10, chacune de ces valeurs devant être écrite avec des 0 et des 1.
La valeur 2 s’écrira 0000000000000010, la valeur 3 s’écrira 0000000000000011, la valeur 4 s’écrira 0000000000000100, la valeur 5 s’écrira 000000000001001, et ainsi de suite jusqu’à la valeur 10 qui s’écrira 0000000000001010.
Si ces 11 prélèvements parmi une infinité de prélèvements possibles donnent bien une idée des valeurs existantes entre 0 et 10, ce choix de seulement 11 valeurs nous fait ignorer les valeurs intermédiaires (par exemple 0,5 V, 1,5 V, 3,8 V, etc.). Pour plus de précision, nous pouvons sélectionner une centaine de valeurs par « pas » de 0,1 V (0,1 V, 0,2 V, 0,3 V, 0,4 V, etc., jusqu’à 10 Volts).
Dans notre exemple, nous allons choisir non pas 10, ni 100 valeurs, mais 65 536 valeurs parmi l’infinité de valeurs possible entre 0 et 10 Volts ! Comme nous venons de le montrer, un codage sur 16 bits met à notre disposition 65 536 valeurs (combinaisons) pour quantifier les 65 536 prélèvements que nous allons faire entre 0 V et 10 V. La quantification, du verbe « quantifier », permet de définir le nombre de bits (chiffres 1 ou chiffres 0) qui va être utilisé pour coder une valeur analogique : par exemple, le chiffre 5 prend la valeur 0101 s’il est quantifié sur 4 bits, mais prend aussi la valeur 00000101 s’il est quantifié sur 8 bits ; le mot binaire de 4 bits et le mot binaire de 8 bits représentent tout deux le chiffre 5, mais dans le cas du mot de 4 bits, 0101 est une combinaison parmi 16 combinaisons possibles (allant de 0000 à 1111), alors que dans le cas du mot de 8 bits, 00000101 est une combinaison parmi 256 combinaisons possibles (allant de 0000000 à 11111111).

Quantification 4 bits / 8 bits
Nous allons maintenant considérer que la valeur maximum analogique 10 Volts (dans notre fourchette de 0 à 10 V) correspond à la valeur maximale numérique sur 16 bits, soit 1111111111111111. La valeur 5 Volts représentera la moitié de cette valeur numérique et s’écrira donc 10000000000000000. Inversement, la valeur numérique prise au hasard 0101000110000001 (20 865 en décimal) correspondra à 20 865 fois la résolution (10 volts / 216 -1) du convertisseur 16 bits, c’est-à-dire 20 865 x 0,0001525, ce qui donne 3,18 V.
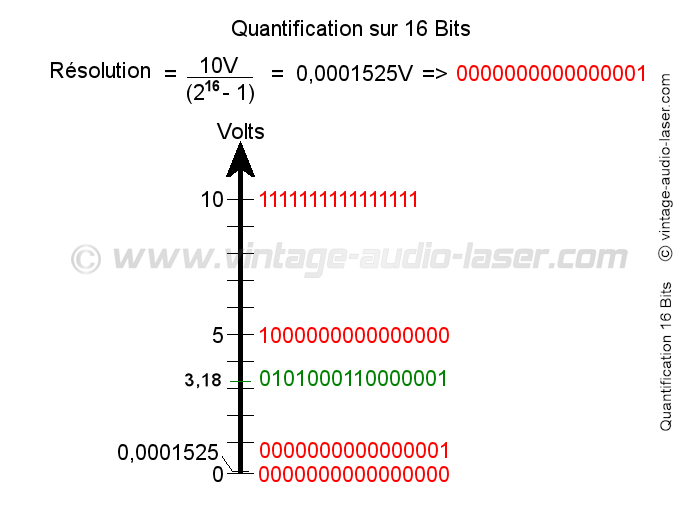
La quantification sur 16 bits d’une plage de tension allant de 0 à 10 Volts nous permet d’obtenir 65 536 niveaux de tensions
Cette valeur analogique (3,18 V) très précise correspond à 1 valeur possible parmi les 65 536 que nous permet la quantification sur 16 bits, pour définir l’ensemble de valeurs comprises entre 0 V et 10 Volts.
numériser un signal analogique, tel que la vitesse d’un véhicule automobile
Choix des valeurs
○ Choisir une valeur maximum : 200 km/h
○ Choisir le nombre de bit « n » qui va servir à coder chaque valeur (quantification) : « n » = 16
○ Définir la résolution : Valeur Maximum ÷ (2n -1), soit 200 ÷ (216 -1) = 0,0030518 km/h
○ La résolution correspond à la valeur du LSB (0000000000000001), ou encore l’écart minimum entre deux valeurs que pourra représenter notre système de conversion
Conversion
○ 160 km/h donne : 160 ÷ 0,0030518 = 52 428
○ 52 428 en binaire donne : 215 + 214 + 211 + 210 + 27 + 26 + 23 + 22 = 32 768 + 16 384 + 2 048 + 1 024 + 128 + 64 + 8 + 4 (chaque puissance de 2 valide un « 1 » correspondant à son rang)
○ 160 km/h correspond à la valeur binaire 1100110011001100, par une quantification sur 16 bits, la valeur maximum 1111111111111111 correspondant à 200 km/h
Note : quand la puissance de 2 augmente de 1 (par exemple, de « 24 » à « 25 »), la valeur décimale correspondante est doublée (de 16 à 32 pour les valeurs de puissances 4 et 5).

Une méthode pour corriger la diminution de la réponse dans les hautes fréquences en contrepartie de l’élimination de l’effet d’aliasing, et les effets du bruit de quantification, est d’introduire la technique du suréchantillonnage en amont du convertisseur N/A, autrement appelée « filtrage numérique ».
Rappelons que les signaux numériques sur le disque sont des mots non-modifiables de 16 bits sous une fréquence d’échantillonnage de 44,1 kHz. En revanche, les techniques employées à l’intérieur du lecteur CD peuvent être modifiées : en utilisant une mémoire additionnelle, (et des lignes à retard et diverses techniques de multiplication), il est possible de calculer des prédictions de mots numériques acceptables pouvant être insérées entre deux échantillons.
Une méthode simple pour fabriquer un mot numérique additionnel pouvant être inséré entre deux échantillons est l’interpolation, décrite plus haut. Cette méthode consiste à faire la somme de deux échantillons consécutifs, à la diviser par deux, et à insérer le mot obtenu entre les deux échantillons de départ.
On trouve aujourd’hui des lecteurs mettant en œuvre un suréchantillonnage x 4, x 8, voire des fréquences d’échantillonnage encore supérieures. L’image ci-dessous montre l’effet de l’échantillonnage x 4 :
Un suréchantillonnage x 4 permet d’obtenir 3 mots numériques prédits, à insérer entre 2 « vrais » échantillons. La fréquence d’échantillonnage est portée à 176,4 kHz et le nombre d’échantillons est multiplié par quatre. Le bruit de quantification est ainsi réduit et expulsé dans les hautes fréquences. Le rapport signal / bruit s’en trouve amélioré
Le filtrage analogique est facilité par le filtrage numérique effectué en amont. Le doublement de la fréquence d’échantillonnage permet l’utilisation d’un filtre conventionnel à pente douce pour retirer le premier sous-harmonique qui devient ainsi 44,1 kHz, ce qui a pour effet d’améliorer la réponse dans les hautes fréquences
Le filtrage numérique permet donc de supprimer l’aliasing, et de diminuer le bruit de quantification, sans le supprimer. Même si celui-ci n’est pas audible, il engendre de la distorsion par intermodulation et un échauffement des composants. Il peut aussi perturber la chaîne d’amplification et détériorer les haut-parleurs du système acoustique. Un artifice consistant à injecter un signal bruité (« dither ») de même amplitude que le bruit de quantification permet de palier ce phénomène.
Note : le suréchantillonnage a été utilisé dès le premier lecteur CD Philips (Philips CD100) avec le circuit intégré SAA7030, en association avec le convertisseur numérique vers analogique TDA1540 (14 bits) : les données séries 16 bits corrigées et séparées (voies gauche et droite) sont suréchantillonnées x 4 ce qui a pour effet de supprimer l’effet d’aliasing, et de réduire le bruit de quantification en sortie du filtre numérique à un niveau équivalent à celui d’un convertisseur « classique » 16 bits. Les données série 14 bits en sortie du SAA7030 sont ensuite envoyées vers deux convertisseurs N/A 14 bits de type TDA1540. L’opération de filtrage analogique est facilitée par ce filtrage en amont des convertisseurs.

Pour retrouver la valeur analogique correspondant à un mot numérique de 16 bits, il est indispensable de connaître la valeur de chaque bit de ce mot.
Aussi, chacun de ces 16 bits représente une puissance de 2. Le LSB (bit de poids le plus faible) représente la puissance de 2 la plus faible (20 = 1), alors que le MSB (bit de poids le plus fort) représente la plus forte (215 = 32768).
Un mot de 16 bits peut prendre n’importe quelle combinaison composée de 1 et de 0 parmi 65 536 combinaisons possibles, allant de 0000000000000000 à 111111111111111.

bit de poids fort (MSB) et bit de poids faible (LSB)
Le LSB dans un mot de 16 bits est : 0000000000000001 ; il s’agit de la plus petite valeur numérique possible, soit 1 en valeur décimale (20).
Le MSB dans un mot de 16 bits est : 1000000000000000 ; Il s’agit de la moitié de la valeur numérique maximum, soit 32 768 (65 536 ÷ 2, avec 65 536 correspondant à 1111111111111111, la valeur numérique maximum possible), en valeur décimale.
En connaissant la valeur de chaque bit de ce mot numérique de 16 bits, nous pouvons calculer la valeur décimale de ce mot.
○ Exemple :
11111111111111111111 = 32 768 + 16 384 + 8 192 + 40 96 + 2 048 + 1 024 + 512 + 256 + 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 65 535
Note : la 65 536ème combinaison est la valeur 0 (soit 0000000000000000)
convertisseur n/a basique à résistances calibrées
Différentes technologies (multi-bits, 1 bit) ont été utilisées pour la conversion numérique / analogique depuis le début de l’ère du CD ; voici le principe de fonctionnement du convertisseur basique multi-bit :
Les mots de 16 bits (ou 14 bits) en provenance du decoder EFM ou du filtre numérique sont envoyés un à un dans le convertisseur numérique / analogique, les 16 bits de chaque mot pouvant être classés du bit de poids le plus faible (LSB) pour le bit le plus à droite (par convention), au bit de poids le plus fort (MSB) pour le bit le plus à gauche.
Précisons qu’en raison d’un éventuel suréchantillonnage en amont, ces mots peuvent contenir beaucoup plus de 16 bits.
Le schéma de base du convertisseur N/A (convertisseur 16 bits sans filtre numérique) comporte une série de générateurs de courant en provenance d’une source de tension très stable (10 Volts par exemple). Chaque générateur de courant est relié à un interrupteur, lui-même relié à un convertisseur courant / tension. Ce dernier est chargé de fournir, en sortie du convertisseur, une tension analogique résultant de la somme des courants qui ont été créés par la fermeture des interrupteurs provoquée par le passage des 1 contenus dans le mot de 16 bits « injecté » à l’entrée du convertisseur. Dans notre exemple, 16 générateurs sont activés par les 16 bits de notre mot de 16 bits, chaque bit « contrôlant » un et un seul générateur de courant correspondant au « poids » du bit (exemple : le troisième bit en partant de la gauche active le 3ème générateur en partant de la gauche — si ce bit est à 1 — par la fermeture de l’interrupteur D3). Chaque générateur fournit une valeur de courant unique.
○ Quel est le rapport entre les différents générateurs de courant ?
Le générateur commuté par le MSB (le générateur le plus à gauche sur le schéma) doit fournir très précisément la moitié de la somme des courants disponibles (courants délivrés par l’ensemble des générateurs). Le générateur suivant (à la droite du précédent, donc) doit fournir aussi précisément la moitié du courant de son voisin de gauche et ainsi de suite jusqu’au 16ème générateur, représentatif du LSB et chargé de délivrer un courant très faible (le 65 536ème du courant total).
Cette haute précision, caractéristique essentielle de la conversion numérique vers analogique, explique les tarifs relativement élevés appliqués à ce type de composants, surtout au début de l’ère du Compact Disc.
Ce type de convertisseur à résistance calibrée voit les interrupteurs (les switchs) se fermer au rythme de l’arrivée des « 1 » contenus dans le mot de 16 bits appliqué à l’entrée. Chaque mot génère donc un courant correspondant à la somme des courants générés par la fermeture successive des interrupteurs. Ce courant global obtenu est ensuite converti en tension, qui doit être la réplique exacte de l’échantillon (le prélèvement) initial (celui correspondant au signal analogique disponible avant le processus de numérisation puis de gravure du disque). Chaque mot numérique appliqué à l’entrée du convertisseur de manière séquentielle permet de restituer ce signal analogique d’origine, la vitesse d’exécution étant fonction de la fréquence d’échantillonnage à laquelle les mots sont appliqués au circuit.
Cependant, ce type de convertisseur N/A, souffre de problèmes inhérents provoquant des irrégularités dans le signal de sortie tels que non-linéarité, distorsion de croisement, et glitches (bruit de transitions). De plus, une altération du générateur de courant correspondant au « bit de poids fort » entraîne une très forte distorsion rendant le signal sonore analogique final pratiquement inaudible. Malheureusement, il est très difficile voire impossible de produire une résistance ayant pour valeur exactement la moitié ou le double de celle de la résistance précédente ou suivante, sans aucune variation dans la plage de tolérance. Par exemple, dans l’illustration ci-dessous, si R1 à une valeur de 5 kΩ, alors R2 doit avoir pour valeur 10 kΩ, R3 20 kΩ, et ainsi de suite jusqu’à R16 qui vaut alors 163,84 MΩ (5 kΩ x 32 768), pour des courants allant de quelques mA à quelques dixièmes de µA (1 / 65 536ème du courant total pour R16, soit 0,06 µA pour Ve = 10 V, 2 mA pour IR1, et donc, 4 mA pour le courant total).
Note : la multiplication par 2 de la valeur d’une résistance permet de diviser par 2 le courant qui la traverse
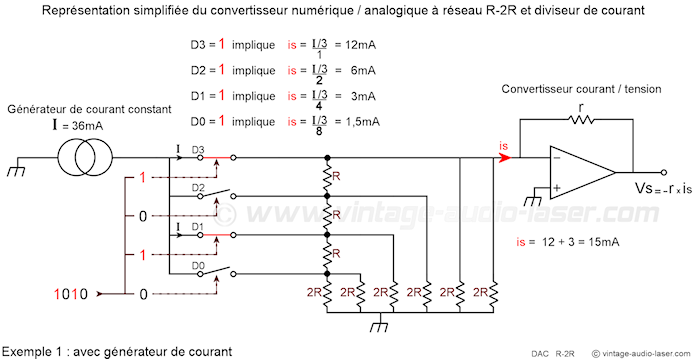
convertisseur n/a à réseau r-2r
La conversion N/A à réseau R-2R est une alternative au principe précédent.
Cette appellation provient du fait que ce type de convertisseur à diviseur de courant n’utilise que deux valeurs de résistance (R et deux fois R), ce qui permet de limiter certains effets produits par le réseau à résistances calibrées décrit ci-dessus. Comme précédemment, chaque bit à « 1 » produit un courant proportionnel au poids de ce bit.
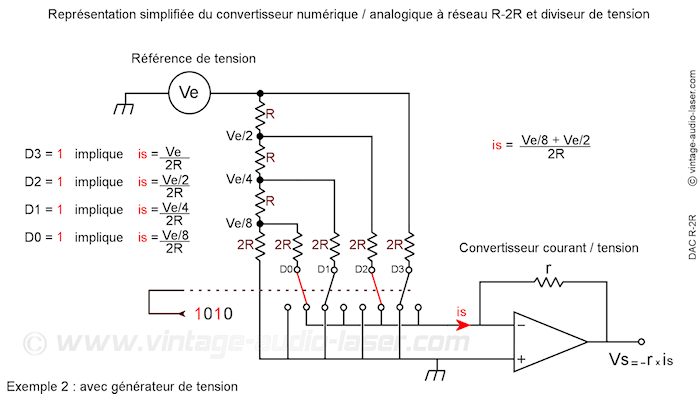
Les 2 schémas ci-dessous illustrent le montage R-2R, à partir d’un générateur de courant constant et à partir d’un générateur de tension parfait.
D’autres méthodes de conversion N/A ont été beaucoup utilisées par les premiers lecteurs CD, telles que la conversion par intégration à double rampe et la conversion DEM (TDA1540, par exemple). En outre, les techniques dites « One bit » ont été développées par la suite, mais ne seront pas abordées ici.
Le convertisseur DEM (Dynamic Element Matching) repose sur le principe du convertisseur N/A à résistances calibrées dans une version améliorée à diviseur de courant. Ce type de convertisseur nécessite plus de composants externes (réseau de condensateurs) mais est plus facile à mettre en œuvre.
Le convertisseur intégrateur à double rampe est plus intéressant, car il aborde un principe différent.
convertisseur intégrateur à double rampe
Le principe de ce convertisseur est le suivant : les mots de 16 bits sont envoyés sous forme d’un signal série un à un dans un compteur numérique intégré au composant. La valeur de départ du compteur correspond à la valeur binaire du mot numérique qui doit être converti. Le temps de décomptage depuis la valeur chargée va déterminer le temps d’intégration du courant délivré par un générateur de courant constant. En fin de décomptage, le générateur de courant est déconnecté et la valeur analogique de l’échantillon est restituée par le condensateur intégrateur.

Principe du convertisseur N/A intégrateur
La base de temps de cette série d’opérations est définie par l’horloge du convertisseur, l’arrivée de chaque bit de l’échantillon dans le compteur numérique se faisant sur les fronts descendants de l’horloge. Or, nous savons que chaque échantillon doit être converti en 10 µs environ, pour satisfaire aux exigences du processus de numérisation du format CD. Ceci permet de définir l’horloge requise pour le traitement d’un mot de 16 bits :
65 535 ÷ (10 x 10-6) = 6,5 GHz
Ce résultat correspond à l’horloge nécessaire, en théorie, pour un décomptage en 10 µs depuis la valeur maximale potentielle d’un échantillon codé sur 16 bits, jusqu’à 0. Évidemment, une telle fréquence n’est pas envisageable. Ainsi, les nombreux convertisseurs numérique / analogique adoptant ce schéma contournent ce problème de fréquence d’horloge trop élevée par la mise en œuvre simultanée de deux compteurs numériques séparés et indépendants activant deux générateurs de courants séparés et de valeurs différentes.
L’échantillon de 16 bits est alors séparé en deux échantillons de 8 bits correspondant respectivement aux 8 bits de poids fort et aux 8 bits de poids faible. Sachant que la valeur maximum que peut prendre un mot de 8 bits est 255 (28-1) et que la conversion simultanée des deux mots de 8 bits doit se faire en 10 µs, l’horloge nécessaire devient :
255 ÷ (10 x 10-6) = 25,5 MHz ©vintage-audio-laser.com
Au vu de ce résultat, on comprend aisément l’intérêt de traiter des mots de 8 bits plutôt que des mots de 16 bits.
Puisque les deux générateurs de courant chargent simultanément le condensateur intégrateur, il est indispensable que le générateur de courant activé par les 8 bits de poids fort puisse délivrer au maximum 256 fois plus de courant que le courant maximum du générateur activé par les 8 bits de poids faible.
Pour 16 bits, le ratio est le suivant : I1Max = 256 × I2Max
Un mot de 16 bits correspondant au LSB 00000000 00000001 ne laissera le courant circuler que très peu de temps, et par conséquent produira une charge du condensateur très faible, correspondant à la résolution du convertisseur (voir plus haut).
Fonctionnement
Après que les compteurs ont été initialisés par les deux mots de 8 bits, les deux commutateurs internes S1 et S2 correspondant aux deux générateurs de courant I1 et I2 (cf. schéma) sont fermés par l’envoi d’un signal de commande de début d’intégration. Les compteurs commencent à décompter depuis les valeurs respectives des deux mots de 8 bits. Le condensateur C se charge, ©vintage-audio-laser.com jusqu’à l’ouverture des commutateurs S1 et S2 (par la commande STOP), chaque commutateur étant ouvert à l’instant où son compteur respectif arrive à 0.
La charge finale du condensateur (Itotal = I1 + I2), qui correspond à la valeur analogique de l’échantillon de 16 bits de départ, est ensuite restituée par la fermeture du commutateur S4 d’entrée du circuit de sample and hold (échantillonnage / blocage) placé en sortie du circuit intégrateur. La dernière opération consiste à décharger le condensateur à l’aide du commutateur S3 (transistor MosFet) externe au convertisseur, la résistance Drain / Source (RDS) interne au transistor jouant le rôle de circuit de décharge. Par suite, un nouvel échantillon est chargé dans le compteur et un nouveau cycle démarre pour une durée de 20 µs, incluant 12 µs pour la génération des deux rampes et 8 µs pour le resampling et le reset (échantillonnage / blocage et décharge de C).
La valeur analogique extrêmement précise restituée, est composée d’une tension plus forte résultant des 8 bits de poids fort, et une tension beaucoup plus faible résultant des 8 bits de poids faible. Le convertisseur numérique / analogique doit être associé à un convertisseur courant / tension optimisé par l’utilisation d’un condensateur intégrateur doté d’excellentes caractéristiques (courant de fuite minimum), et un AOP à très forte impédance d’entrée.
Au début du temps t1, S1 et S2 sont fermés. À la fin du temps a, S2 est ouvert stoppant le générateur activé par les 8 bits de poids faible. La pente de charge diminue, car seul le générateur activé par les 8 bits de poids fort continue de charger le condensateur C jusqu’à la fin du temps b et l’ouverture de S1. Au début du temps t2, S4 est fermé et la charge de C est envoyée dans l’échantillonneur / bloqueur (E/B). La fin du temps t2 correspond à l’ouverture de S4 qui isole l’intégrateur de l’E/B. Au temps t3, la commande de décharge est envoyée sur le transistor qui décharge C. Au même moment, un nouvel échantillon est chargé dans le compteur
Précisions que ce circuit externe est doublé dans le cas d’une conversion de données stéréos, effectuée par le traitement alternatif des échantillons gauche et droit. Les courants respectifs Igauche et Idroit sont alors disponibles sur deux broches de sortie du convertisseur.
Le convertisseur numérique / analogique intégrateur à double rampe CX20017 (d’origine Sony) équipe de nombreux lecteurs CD de 1ère et 2ème générations tels que le Sony CDP-101 ou encore le Yamaha CD1.
erreur de linéarité
Chaque générateur de courant est généralement constitué d’un réseau de résistances délivrant un courant d’une valeur spécifique et chaque générateur doit être une fraction de celui qui le précède. Ainsi, si le générateur de courant pour le MSB est prévu pour délivrer la moitié du courant total disponible alors le générateur suivant doit à son tour fournir la moitié du courant délivré par le générateur MSB et ainsi de suite. La moindre variation hors tolérance empêche une reproduction fidèle du signal analogique d’origine.
bruits de transition (glitches)
Les bruits de transition sont occasionnés par les fermetures des « switchs » actionnés par les bits à « 1 », à l’intérieur du convertisseur N/A. Dans la plupart des cas, le signal analogique en sortie du convertisseur N/A est appliqué à un circuit de « deglitching » pour retirer les interférences indésirables générées pendant le système de conversion. Ce circuit « deglitcher » est un échantillonneur / bloqueur (Sample and hold). Il s’agit d’une mémoire analogique de tension, généralement utilisée pour la conversion analogique vers numérique : l’échantillon « n+1 » est bloqué pendant le temps de conversion de l’échantillon « n ».
L’échantillonneur bloqueur (sample & hold) est utilisé comme « deglitcher » afin de supprimer les bruits de transition (glitches) en sortie du convertisseur numérique / analogique
Cette étude globale du fonctionnement du lecteur CD est terminée. Cette fabuleuse technologie est disponible gratuitement dans votre déchetterie ou pour une poignée d’€uros sur votre site de petites annonces préféré.
Si vous souhaitez un complément d’information, ou apporter une précision ou une correction à cet article (errare humanum est), merci d’utiliser la page contact.
Respectez les droits d’auteur,
Denis / novembre 2011.




















 RECHERCHE
RECHERCHE

MESSAGES
1. La technique du lecteur CD... (page 4), 19 mai, 16:20, par gerard beot
bonjour
merci pour votre description du lecteur cd c est très intéressant. ou peut t on se procurer une copie de ces pages ou un livre en Français sur se sujet .je vous re merci pour cela
cordialement
gerard beot
1. La technique du lecteur CD... (page 4), 19 mai, 23:29, par LD50
Bonjour,
Cet article n’est disponible qu’ici même. Il peut être consulté à volonté et sa disparition n’est pas au programme :)
Cordialement